En la ciencia de los materiales, se pueden utilizar descriptores tanto controlables como incontrolables para describir la naturaleza de los materiales. Entre los ejemplos de descriptores controlables, se encuentran la composición de elementos y procesos de fabricación; por el contrario, los descriptores incontrolables se generan a partir de datos experimentales que describen la naturaleza de muestras particulares, como datos espectrales sin procesar o el peso específico. En este estudio, se considera un diseño experimental para obtener un modelo predictivo de alta precisión en el que los descriptores incontrolables de los materiales son características y sus propiedades materiales son etiquetas. En general, dado que los descriptores incontrolables están más estrechamente relacionados con las propiedades de los materiales, las predicciones basadas en ellos serán más precisas. El objetivo del diseño experimental en el presente estudio no es la mejora de las propiedades del material como tal, sino la predicción de sus propiedades.
Para desarrollar este diseño, hemos seleccionado descriptores controlables apropiados para la síntesis del material candidato que mejoran la precisión de la predicción cuando se incorporan a los datos de entrenamiento los descriptores incontrolables correspondientes y las propiedades del material. Proponemos dos métodos de diseño experimental: uno basado en la optimización bayesiana y el otro en el muestreo de incertidumbre. Utilizando una base de datos de polímeros en la que se registran descriptores controlables e incontrolables y propiedades mecánicas, confirmamos que nuestro método puede seleccionar un material candidato apropiado para entrenar un modelo predictivo de alta precisión en el que las propiedades del material se predicen a través de descriptores incontrolables. El método que proponemos se puede aplicar a desarrollos de materiales en los que los descriptores incontrolables se obtienen de manera más sencilla mediante experimentos que obteniendo propiedades del material objetivo; también será útil para extraer la relación entre la estructura y las propiedades de un material.
Introducción
Se han reportado varias aplicaciones exitosas del aprendizaje automático en la ciencia de los materiales [1-18]. En particular, las predicciones que utilizan modelos de regresión de aprendizaje automático son convincentes para la ciencia de los materiales porque las propiedades de materiales que aún no se han sintetizado se pueden predecir sin su síntesis y medidas reales. Para realizar una investigación exitosa utilizando predicciones de aprendizaje automático, es importante construir un modelo de regresión de alta precisión con un conjunto de datos de entrenamiento. En general, la precisión del modelo de regresión depende, en gran medida, de la cantidad de datos de entrenamiento. Sin embargo, en la ciencia de los materiales, la obtención de datos requiere una cantidad de tiempo significativa y costes elevados. Por consiguiente, es un desafío crear modelos predictivos precisos con la menor cantidad posible de datos de entrenamiento.
Una estrategia fiable para obtener un modelo predictivo preciso es la selección de características, que busca características importantes que incrementen el rendimiento de la predicción [19-22]. En este estudio, sin embargo, nos centramos en otra estrategia: el aprendizaje activo, que selecciona nuevos puntos de datos que se incorporarán al conjunto de datos de entrenamiento para mejorar la precisión de la predicción. Aquí, se seleccionan nuevos datos de los materiales candidatos, que no se han sintetizado, preparados de antemano. El muestreo de incertidumbre en el aprendizaje activo es útil: se selecciona el punto de datos con las incertidumbres más altas para mejorar la precisión de la predicción [23-27]. Por ejemplo, estas incertidumbres corresponden a las desviaciones de los valores previstos, evaluadas mediante regresión del proceso gaussiano.
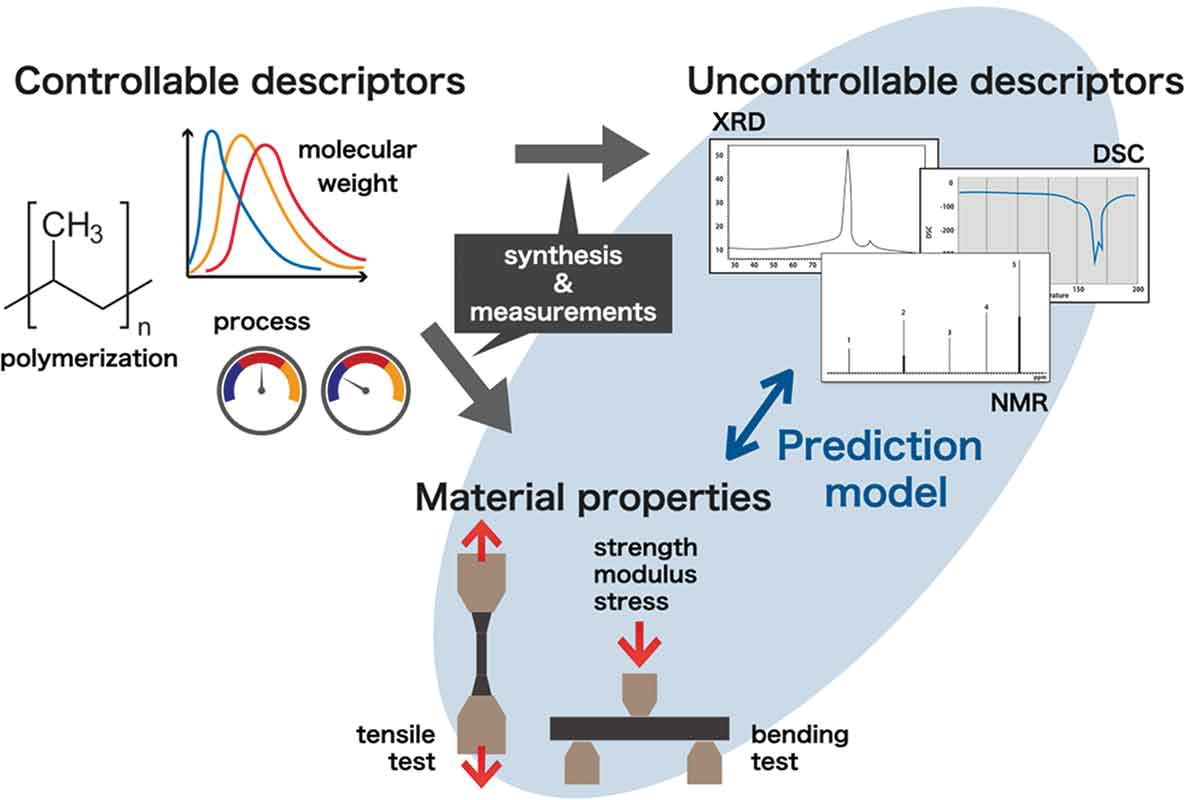
Sin embargo, el muestreo de incertidumbre no siempre es posible en problemas surgidos en la ciencia de los materiales. Como característica de la ciencia de los materiales, se pueden usar dos tipos de descriptores de materiales como características al entrenar el modelo de regresión (ver Figura 1). El primer tipo son los descriptores controlables, que se pueden elegir de antemano sin sintetizar el material, como composiciones de elementos y procesos de fabricación. El segundo tipo son los descriptores incontrolables, aquellos que se generan a partir de datos experimentales, como los datos espectrales sin procesar y el peso específico de las muestras y, por lo tanto, se desconocen sin síntesis. Si las características utilizadas para los modelos de regresión se limitan a descriptores controlables, se puede seleccionar un nuevo punto para mejorar la precisión de la predicción mediante un muestreo de incertidumbre convencional. Esto se debe a que, cuando las características son descriptores controlables, sus valores fundamentales se conocen de antemano y, por lo tanto, la incertidumbre (evaluada mediante una predicción específica de aprendizaje automático) se define de manera exacta, incluso si el material no se ha sintetizado realmente. Por otro lado, cuando se utilizan descriptores incontrolables como características, la situación cambia por completo: como el conjunto de datos candidato no puede prepararse para descriptores incontrolables sin síntesis y mediciones, es imposible la selección de descriptores incontrolables mediante muestreo de incertidumbre convencional.
Este estudio busca obtener un modelo predictivo altamente preciso de las propiedades de los materiales a partir de descriptores incontrolables con la menor cantidad posible de experimentos. En general, las dimensiones de los descriptores incontrolables generados por los datos experimentales se pueden incrementar realizando varias mediciones, y los descriptores incontrolables, en muchos casos, están más estrechamente relacionados con las propiedades de los materiales. Por lo tanto, el uso de descriptores incontrolables debería mejorar la precisión de la predicción. Además, si se obtienen descriptores incontrolables con más facilidad que las propiedades del material objetivo, se pueden predecir datos experimentales difíciles de medir a partir de datos fáciles de medir. Este modelo se puede utilizar de varias maneras (por ejemplo, optimización de materiales y reutilización de materiales), como se debatirá en el apartado “Debate y resumen”. Además, utilizando el modelo predictivo, se puede comprender la relación entre la estructura expresada por los descriptores incontrolables y las propiedades de un material.
La metodología del diseño experimental propuesto en este estudio es la siguiente. En primer lugar, preparamos un conjunto de datos candidato que se construye utilizando solo descriptores controlables. Cuando se selecciona un descriptor controlable, los descriptores incontrolables y las propiedades del material objetivo se obtienen sintetizando el material y realizando mediciones. Posteriormente, entrenamos un modelo de regresión para predecir la propiedad objetivo a partir de los descriptores incontrolables sin usar los controlables. A continuación, seleccionamos los descriptores controlables apropiados a partir del conjunto de datos candidato de modo que la precisión del modelo predictivo que usa los descriptores incontrolables sea alta. Desafortunadamente, el método de muestreo por incertidumbre convencional no se puede utilizar directamente en esta etapa y, por lo tanto, es necesario desarrollar un nuevo método. Proponemos dos métodos para utilizar descriptores incontrolables en el aprendizaje activo: uno basado en la optimización bayesiana y otro basado en el muestreo de incertidumbre. Para demostrar el rendimiento de estos métodos, en este estudio se utiliza un conjunto de datos de polipropileno.
Método de diseño experimental
Establecimiento del problema
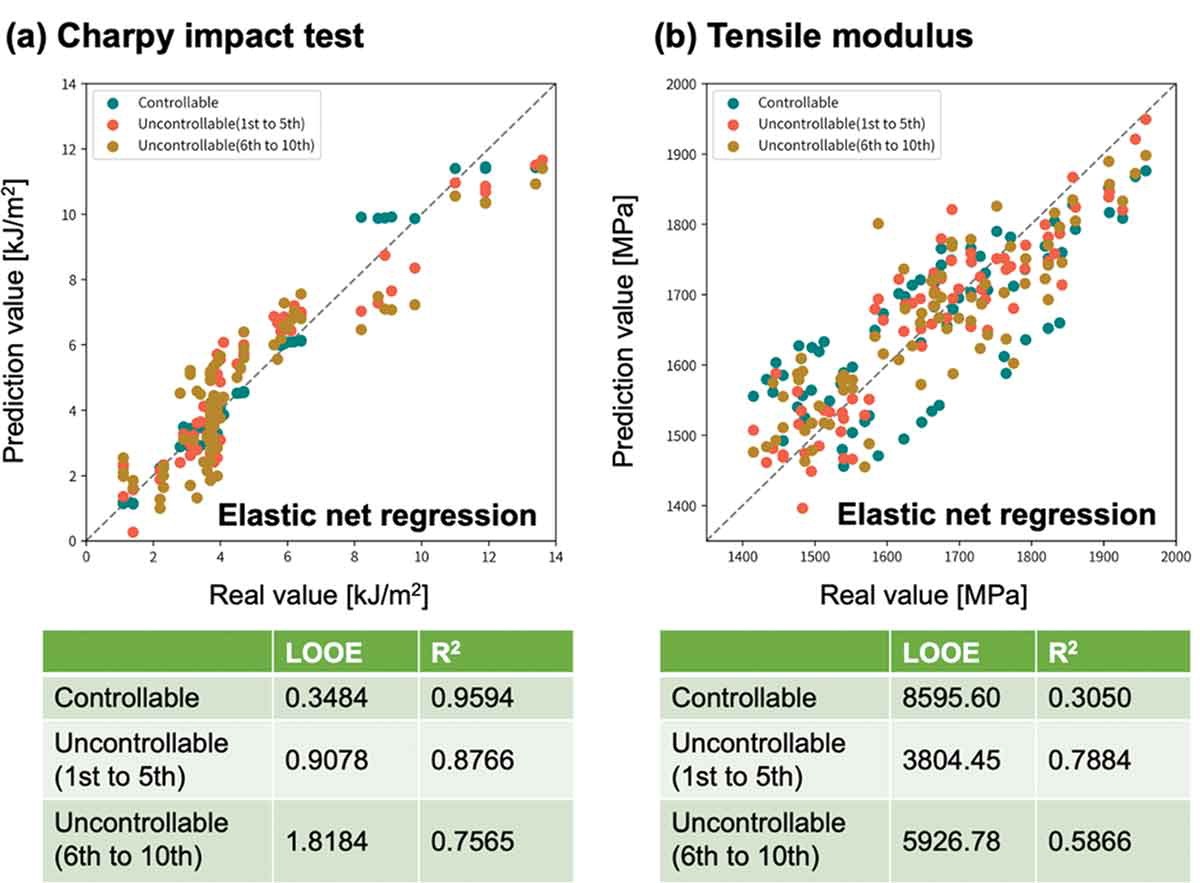
Los descriptores controlables e incontrolables están representados por xi ∈ Rd y x′i ∈ Rd, respectivamente; yi ∈ R es la propiedad del material de destino. En primer lugar, preparamos un conjunto de datos construido usando solo los descriptores controlables de los materiales candidatos; esto se expresa como Dc = {xi}i = 1,…,N, donde el número de materiales candidatos es N. Asumimos que, para solo descriptores controlables M en Dc, expresados como Dc,M = {xk} k=1,…,M, los descriptores incontrolables {x′k}k=1,…,M y las propiedades objetivo {yk}k=1,…,M se obtienen experimentalmente. Los datos de entrenamiento para el modelo de regresión se expresan como D′t,M = {x′k, yk}k=1,…,M. El rendimiento predictivo de este modelo de regresión, en el que los descriptores incontrolables son características y las propiedades de destino son etiquetas, se evalúa mediante el método de validación cruzada dejando uno fuera. Para mejorar el rendimiento de la predicción, seleccionamos el siguiente material candidato apropiado caracterizado por los descriptores controlables del conjunto de datos restante en Dc∖Dc,M, donde el número de puntos de datos viene determinado por N − M. El conjunto de datos para los descriptores controlables y las propiedades objetivo, cuando el número de puntos de datos es M, se indica como Dt,M = {xk, yk}k=1,…,M.
Método basado en optimización bayesiana
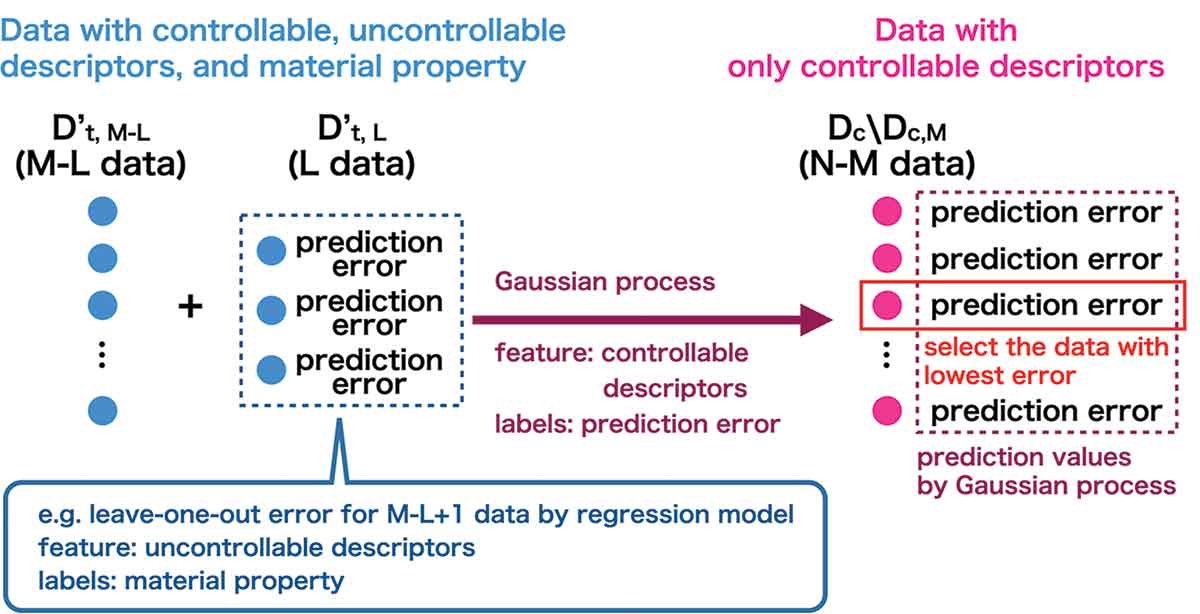
En esta sección, presentamos un método basado en la optimización bayesiana. Se consideran los siguientes pasos para seleccionar los datos M+1st usando este esquema. En primer lugar, el conjunto de datos de entrenamiento, D′t,M, se divide aleatoriamente en un conjunto de datos M − L y un conjunto de datos L, que se indican como D′t,M−L y D′t,L, respectivamente, donde L es un hiperparámetro. Los conjuntos de datos correspondientes para los descriptores controlables se indican como Dc,M−L y Dc,L, que se construyen mediante la división de Dc,M. En segundo lugar, se extrae un punto de datos de D′t,L. Usamos este punto de datos extraído y D′t,M–L como datos de entrenamiento para crear el modelo de regresión. La precisión de la predicción del modelo de regresión entrenado se evalúa utilizando el error dejando uno fuera calculado mediante el error cuadrático medio (MSE). En tercer lugar, para cada punto de datos en D′t,L, se realiza el segundo paso. En cuarto lugar, se entrena la regresión del proceso gaussiano utilizando los descriptores controlables en Dc,L como características y las precisiones de predicción evaluadas previamente como etiquetas. La cantidad de datos de entrenamiento se indica mediante L. En quinto lugar, de Dc,∖Dc,M, en términos de optimización bayesiana utilizando la regresión del proceso gaussiano entrenado del paso anterior, se selecciona un único punto de datos para minimizar la precisión de la predicción. Aquí, la mejora esperada (EI) se utiliza como función de adquisición. Finalmente, para los datos seleccionados, mediante experimentos se obtienen los descriptores incontrolables y las propiedades del material. El número de datos conocidos se convierte en M+1, y los conjuntos de datos se actualizan a Dc,M+1 y D′t,M+1. Usando el conjunto de datos D′t,M+1 como datos de entrenamiento, construimos un modelo de regresión en el que las propiedades del material se prevén mediante descriptores incontrolables. Se evalúa la precisión de la predicción de este modelo de regresión. El modelo de regresión debe ser el mismo que se utilizó en el paso dos.
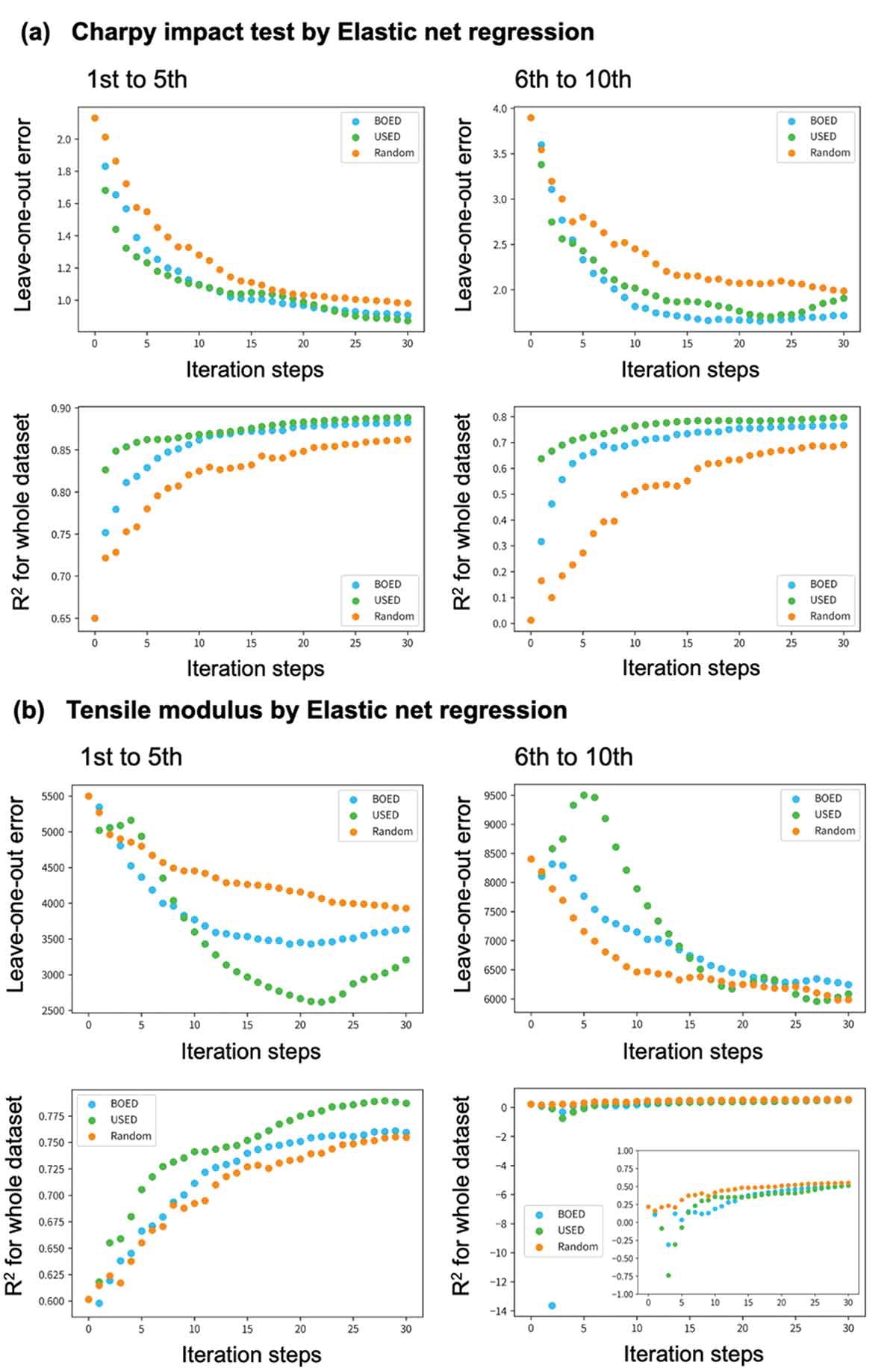
Este método selecciona un punto de datos st M+1 que mejora la precisión de la predicción cuando el punto de datos seleccionado se incorpora al conjunto de datos D′t,M−L, no a D′t,M. El objetivo original es seleccionar el siguiente punto de datos que se incorporará al conjunto de datos D′t,M. Por lo tanto, nuestro algoritmo propuesto se considera una aproximación a este objetivo original. Reducir L para acercar D′t,M−L a D′t,M mejoraría esta aproximación. Sin embargo, la regresión del proceso gaussiano tiene datos de entrenamiento L, por lo que reducir L empeorará su rendimiento de predicción. Por lo tanto, L debe ajustarse en una compensación para encontrar el mejor valor. El pseudocódigo de este método de diseño experimental basado en optimización bayesiana (BOED) se muestra en el Algoritmo 1, y el esquema de BOED se muestra en la Figura 2, donde los puntos de datos M son los datos conocidos.
Para poder ver el contenido completo tienes que estar suscrito. El contenido completo para suscriptores incluye informes y artículos en profundidad